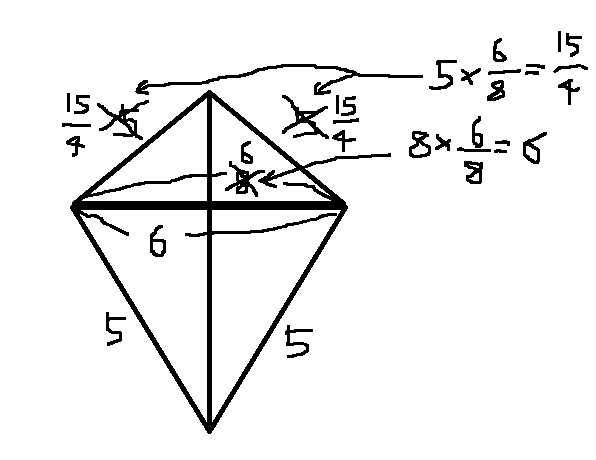|
多くの方が一度は目にしたことはあるであろうギャンブル漫画、「カイジ」。 その作者、福本伸行がカイジをそのまま少年誌風に描いた「ギャンブル+謎解き漫画」こそが「賭博覇王伝 零」だと言えます。 カイジと違うのは、1つ当たりのゲーム時間が短いので、テンポよくたくさんのゲームが次々に出てくること。 あとは、物語が進むにつれて仲間が増えていくところなんかは実に少年誌っぽいです。 実はカイジよりもバランスが良く、万人受けする漫画ではないかなと思います。
賭博覇王伝 零 1
amzn.to
396円
(2022年12月25日 06:53時点
詳しくはこちら)
Amazon.co.jpで購入する
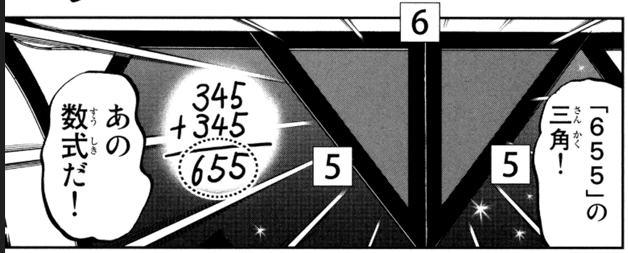
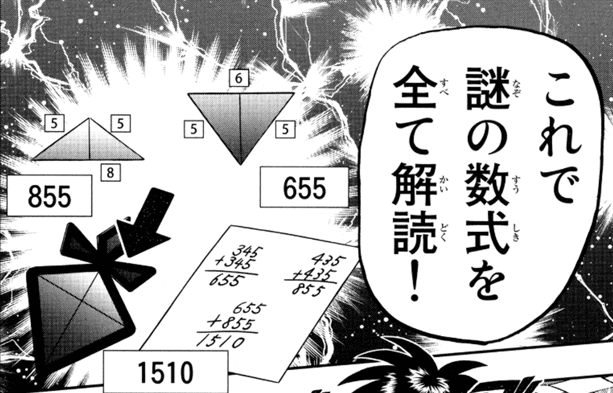
で今回はその「零」について。 「賭博覇王伝 零 ギャン鬼編」を読んでいて思ったことを書いていきます。 内容は、後半の宝探しのパートについてです。 このパートでは色々とツッコミ所はありますが、今回触れるのはある1つの謎解きについて。 というのは、1510(いちごいれ)の謎解きのこと。 1510の謎解き?ギャン鬼編をざっくり説明すると、後半、行方不明の社長「喜十郎」を家族と共に捜索するパートがあります。 そして同時に、その喜十郎の居場所に「宝」があるとの情報があり、「宝探しと捜索」、2重の目的で主人公たちは動くわけです。 ここでは謎解きを勧めながら、喜十郎の居場所に迫っていく展開となり、非常に読み応えのあるパートになっています。 で、そのラスト、喜十郎の監禁部屋に入る直前の、最後の謎解き。 その謎解きをするために、ステンドグラスが壁一面にちりばめられた部屋に入ることに。 そこでは、3つの筆算を使った謎解きをすることになるんです。
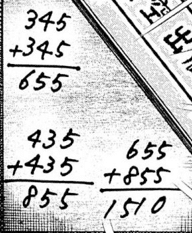
↑これら3つの筆算の謎。 さあ画像を見てみると分かりますが、この筆算のうち、答えが655と855の筆算は計算が合っていません! 345+345は655じゃない!し 一方、1510の筆算は、655+855=1510なので合っている! どういうことだってばよ! 、、、 これについては本記事の主題ではないので、早速答えを言ってしまいます。 、、、 上記3つの筆算は、 「『各辺の長さが3と4と5の直角三角形』を2つ合わせると『各辺の長さ655または855の二等辺三角形』になる。」 ということを意味しています。 つまり345という数字が意味するのは、「斜辺が5で、残りの辺は3と4の直角三角形」です。 その「345の直角三角形」を2つ用意して、345のうち「3」の辺同士を合わせると、「655の"二等辺"三角形」になるし、 「4」の辺同士を合わせると、「855の"二等辺"三角形」になる、ということ。(435+435=855) (文字の説明だと分かりにくいですが、下の方に画像があるので参考にしてください。) で、上記の筆算の意味通り、主人公達、零一行が入っていったステンドグラスの部屋には、345の三角形のステンドグラスが確かにありました。 345の三角形が2つ、対(つい)になった配置です。 その対になった配置の三角形のステンドグラスを移動させ、組み合わせる。すると655の三角形になり、その三角形はポロっと取れます。
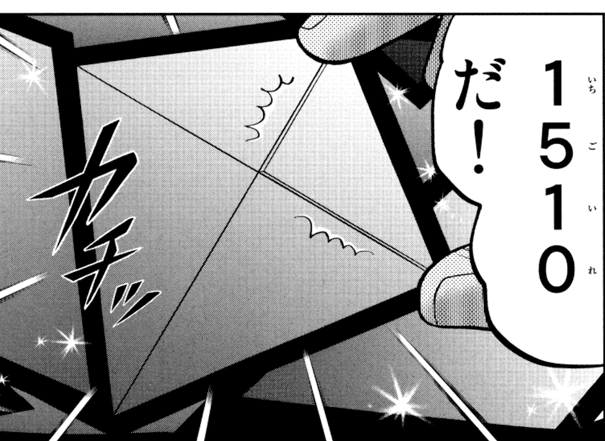
これで2つ「345の三角形」をゲット。 さらに、探してみると、もう1か所、「345の三角形」が2つ対(つい)になった配置が見つかりました。 この三角形のステンドグラスを合わせると、今度は855の三角形になり、これまた同じようにポロっと取れます。 これで合計4つの三角形を入手。 この4つの三角形を使って何をするのかと言うと、合体。 零達が探してみると、ステンドグラスによって作られた絵の中で、イチゴの装飾があるはずの位置にくぼみがありました。 ちょうど何かをはめる為に空いているようなくぼみ。 そこに先ほど入手した、4つの三角形を当てはめてみると、、三角形はぴったりとはまり、四角形のイチゴになったのです。 零:「1510(いちごいれ)だ!」
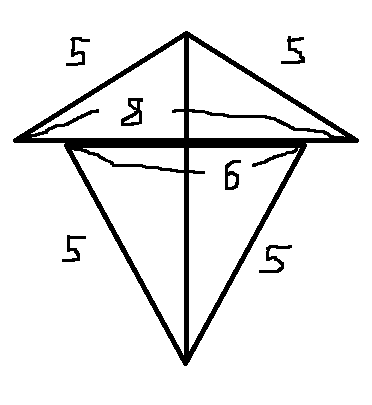
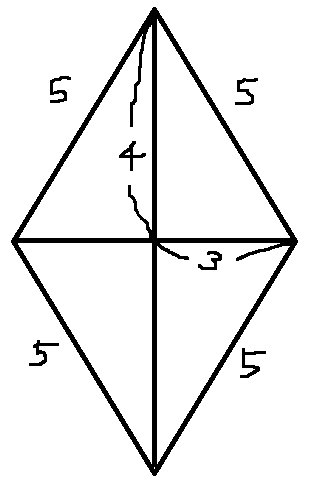
私:(イチゴ入れって!!魔女の館編の見殺さナインとほぼ同レベルやん!!) 、、、そういったツッコミはこの際、さて置きます。 気になってしまったのは別の所で、イチゴの形です。 私:(ん?855の三角形と655の三角形を合わせてイチゴの形を作ろうとすると、8の辺と6の辺が合わなくないか??) そう思ったわけです。 つまり、私の脳内シミュレーションではこうなってしまいます↓
先ほどの漫画のイチゴの形と違います。 仮に855の三角形と、655の三角形をバラして「345の三角形×4つ」にしたところで、どう組み合わせてもひし形になるだけ↓
これも漫画に出てきたイチゴ型(四角形)とは違う。。 うーん?? ここ既読の方々は気にならなかったでしょうか。 サラッと読み飛ばした方もいれば、当たり前のように理解しつつ読んだ方もいるはず。 ただ私にとっては、この1510(イチゴ入れ)の分かりにくさはやや引っ掛かりました。 福本漫画は割とこういった部分を細かく説明してくれるのでここは、あれ?となりました。 では、ここは作者のミスか?と言うと、そうではありません。 漫画内の説明では分かりにくいですが、855の三角形と、655の三角形は大きさが違うんです。 どういうことかを説明する前に、状況を整理しましょう。 元々、「855の三角形」と「655の三角形」はどちらも「345の三角形を2つ組み合わせたもの」でした。 「855の三角形」は、「345の三角形×2つ」を4の辺同士でくっつけたものです。 そして「655の三角形」は、「345の三角形×2つ」を3の辺同士でくっつけたもの。 したがって、仮に「855と655の三角形」を「4つの三角形」にバラした場合、4つ全てが「345の三角形」になるのです。 ただし。 この「4つの三角形」とは、全て同じ「345の”長さ”の三角形」というわけではないんです。 実は「655に使われてる345の三角形」より、「855に使われてる345の三角形」の方が少し小さい、ということになるんですよ。
↓でもこの下の描写だと、855や655という数字を「長さ」だと認識してしまいそうになります。
が、あくまで855や655というのは同じ三角形における「辺の長さの比率」です。 つまり855と655を別々に考えなければいけません。 比率をどちらかに合わせてやらなければならない。 ↓したがって、こういうこと。
655に855の比率を合わせるなら、長さは8:5:5ではなく6:(15/4):(15/4)になるんです!(細けぇ!) つまり最終的に完成するイチゴ型の四角形の4辺の長さは、 5、5、15/4、15/4 になる はい! 、、、 、、、、、、 、、、、、、、、、 これが言いたかっただけです!!(ドテッ!) 結論結論:説明不足ではあるが、三角形を合わせると、ちゃんと漫画内のイチゴの形になる。 、、、 、、、、、、 、、、、、、、、、 (あれ?でも345+345=655や、435+435=855は長さが一致しているのに、855+655=1510では比率の話になるのがなんかしっくりこない。あとやっぱり急に語呂合わせになるのもおかしいし。それと、、) (责任编辑:) |